变分贝叶斯高斯混合(BayesianGaussianMixture)
| 组件名称 | 变分贝叶斯高斯混合(BayesianGaussianMixture) | ||
|---|---|---|---|
| 工具集 | 机器学习/分类/变分贝叶斯高斯混合(BayesianGaussianMixture) | ||
| 组件作者 | 雪浪云-燕青 | ||
| 文档版本 | 1.0 | ||
| 功能 | 变分贝叶斯高斯混合(BayesianGaussianMixture)算法 | ||
| 镜像名称 | ml_components:3 | ||
| 开发语言 | Python |
组件原理
变分贝叶斯方法最早由Matthew J.Beal在他的博士论文《Variational Algorithms for Approximate Bayesian Inference》中提出,作者将其应用于隐马尔科夫模型,混合因子分析,非线性动力学,图模型等。变分贝叶斯是一类用于贝叶斯估计和机器学习领域中近似计算复杂(intractable)积分的技术。它主要应用于复杂的统计模型中,这种模型一般包括三类变量:观测变量(observed variables, data),未知参数(parameters)和潜变量(latent variables)。在贝叶斯推断中,参数和潜变量统称为不可观测变量(unobserved variables)。变分贝叶斯方法主要是两个目的:
- 近似不可观测变量的后验概率,以便通过这些变量作出统计推断。
- 对一个特定的模型,给出观测变量的边缘似然函数(或称为证据,evidence)的下界。主要用于模型的选择,认为模型的边缘似然值越高,则模型对数据拟合程度越好,该模型产生Data的概率也越高。
对于第一个目的,蒙特卡洛模拟,特别是用Gibbs取样的MCMC方法,可以近似计算复杂的后验分布,能很好地应用到贝叶斯统计推断。此方法通过大量的样本估计真实的后验,因而近似结果带有一定的随机性。与此不同的是,变分贝叶斯方法提供一种局部最优,但具有确定解的近似后验方法。
从某种角度看,变分贝叶斯可以看做是EM算法的扩展,因为它也是采用极大后验估计(MAP),即用单个最有可能的参数值来代替完全贝叶斯估计。另外,变分贝叶斯也通过一组相互依然(mutually dependent)的等式进行不断的迭代来获得最优解。

组件
- 组件图:

输入桩
支持单个csv文件输入。
输入端子1
- 端口名称:训练数据
- 输入类型:Csv文件
- 功能描述: 输入用于训练的数据
输入端子2
- 端口名称:用户提供的协方差分布的先验数据
- 输入类型:npy文件
- 功能描述: 输入提供的协方差分布的先验数据据,可以不连
输出桩
支持sklearn模型输出。
输出端子1
- 端口名称:输出模型
- 输出类型:sklearn模型
- 功能描述: 输出训练好的模型用于预测
参数配置
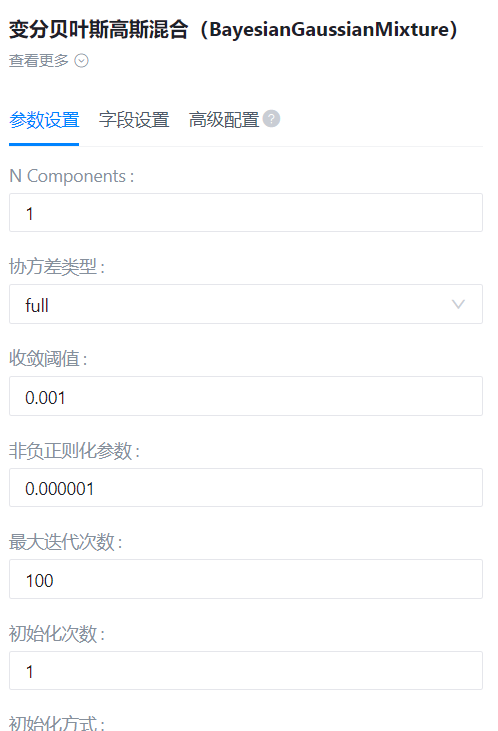
N Component
- 功能描述:混合成分的数量
- 必选参数:是
- 默认值:1
协方差类型
- 功能描述:协方差类型
- 必选参数:是
- 默认值:full
收敛阈值
- 功能描述:收敛阈值
- 必选参数:是
- 默认值:0.001
非负正则化参数
- 功能描述:添加到协方差对角线的非负正则化
- 必选参数:是
- 默认值:0.000001
最大迭代次数
- 功能描述:训练时执行的最大迭代次数
- 必选参数:是
- 默认值:100
初始化次数
- 功能描述:要执行的初始化次数
- 必选参数:是
- 默认值:1
初始化方法
- 功能描述:初始化方法
- 必选参数:是
- 默认值:kmeans
权重浓度先验类型
- 功能描述:权重浓度先验类型
- 必选参数:是
- 默认值:dirichlet_process
权重浓度先验
- 功能描述:权重分布上各组的狄利克雷浓度
- 必选参数:否
- 默认值:(无)
平均分布精度先验
- 功能描述:平均分布精度先验
- 必选参数:否
- 默认值:(无)
平均分布先验
- 功能描述:平均分布先验
- 必选参数:否
- 默认值:(无)
自由度先验
- 功能描述:自由度先验
- 必选参数:否
- 默认值:(无)
Random State
- 功能描述:随机种子
- 必选参数:否
- 默认值:(无)
需要训练
- 功能描述:该模型是否需要训练,默认为需要训练。
- 必选参数:是
- 默认值:true
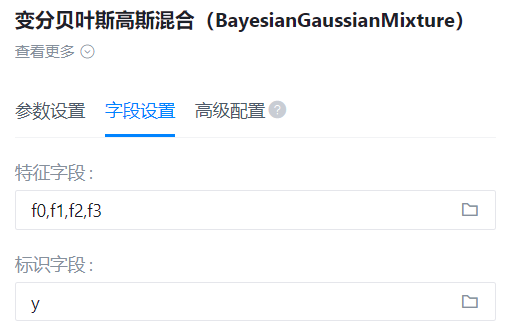
特征字段
- 功能描述:特征字段
- 必选参数:是
- 默认值:(无)
识别字段
- 功能描述:识别字段
- 必选参数:是
- 默认值:(无)
使用方法
- 将组件拖入到项目中
- 与前一个组件输出的端口连接(必须是csv类型)
- 点击运行该节点
测试用例
模板
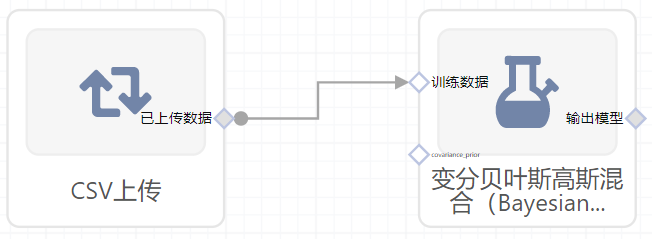
右面板配置
- 参数设置:
- 字段设置:
输入的数据:
输出的结果:
- 输出模型: