带交叉验证的逻辑回归(LogisticRegressionCV)使用文档
| 组件名称 | 带交叉验证的逻辑回归(LogisticRegressionCV) | ||
|---|---|---|---|
| 工具集 | 机器学习 | ||
| 组件作者 | 雪浪云-墨文 | ||
| 文档版本 | 1.0 | ||
| 功能 | 带交叉验证的逻辑回归(LogisticRegressionCV)算法 | ||
| 镜像名称 | ml_components:3 | ||
| 开发语言 | Python |
组件原理
交叉验证,有的时候也称作循环估计(Rotation Estimation),是一种统计学上将数据样本切割成较小子集的实用方法,该理论是由Seymour Geisser提出的。在给定的建模样本中,拿出大部分样本进行建模型,留小部分样本用刚建立的模型进行预报,并求这小部分样本的预报误差,记录它们的平方加和。这个过程一直进行,直到所有的样本都被预报了一次而且仅被预报一次。把每个样本的预报误差平方加和,称为PRESS(predicted Error Sum of Squares)。
交叉验证的基本思想是把在某种意义下将原始数据(dataset)进行分组,一部分做为训练集(train set),另一部分做为验证集(validation set or test set)。首先用训练集对分类器进行训练,再利用验证集来测试训练得到的模型(model),以此来做为评价分类器的性能指标。
1.什么是逻辑回归
逻辑回归就是这样的一个过程:面对一个回归或者分类问题,建立代价函数,然后通过优化方法迭代求解出最优的模型参数,然后测试验证我们这个求解的模型的好坏。
Logistic回归虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别)
回归模型中,y是一个定性变量,比如y=0或1,logistic方法主要应用于研究某些事件发生的概率
2.逻辑回归的优缺点
优点:
- 速度快,适合二分类问题
- 简单易于理解,直接看到各个特征的权重
- 能容易地更新模型吸收新的数据
缺点:
对数据和场景的适应能力有局限性,不如决策树算法适应性那么强
3. 逻辑回归和多重线性回归的区别
Logistic回归与多重线性回归实际上有很多相同之处,最大的区别就在于它们的因变量不同,其他的基本都差不多。正是因为如此,这两种回归可以归于同一个家族,即广义线性模型(generalizedlinear model)。 这一家族中的模型形式基本上都差不多,不同的就是因变量不同。这一家族中的模型形式基本上都差不多,不同的就是因变量不同。
- 如果是连续的,就是多重线性回归
- 如果是二项分布,就是Logistic回归
- 如果是Poisson分布,就是Poisson回归
- 如果是负二项分布,就是负二项回归
4. 逻辑回归用途
- 寻找危险因素:寻找某一疾病的危险因素等;
- 预测:根据模型,预测在不同的自变量情况下,发生某病或某种情况的概率有多大;
- 判别:实际上跟预测有些类似,也是根据模型,判断某人属于某病或属于某种情况的概率有多大,也就是看一下这个人有多大的可能性是属于某病。
5. Regression 常规步骤
- 寻找h函数(即预测函数)
- 构造J函数(损失函数)
- 想办法使得J函数最小并求得回归参数(θ)
6. 构造预测函数h(x)
Logistic函数(或称为Sigmoid函数),函数形式为:
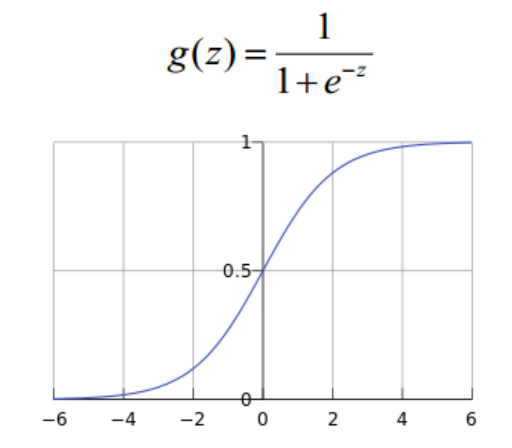
对于线性边界的情况,边界形式如下:
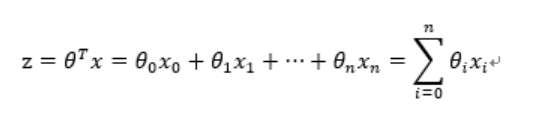
其中,训练数据为向量
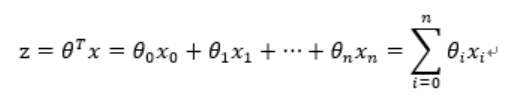
最佳参数
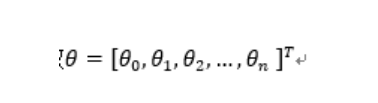
构造预测函数为:
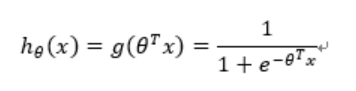
函数h(x)的值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
P(y=1│x;θ)=h_θ (x)
P(y=0│x;θ)=1-h_θ (x)
构造损失函数J(m个样本,每个样本具有n个特征)
Cost函数和J函数如下,它们是基于最大似然估计推导得到的。
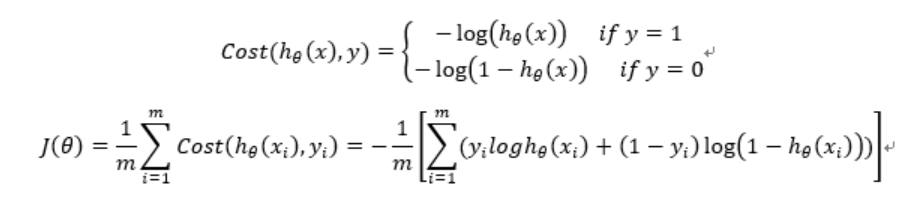
8. 损失函数详细推导过程
概率综合起来写成:
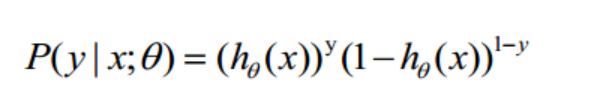
取似然函数为:
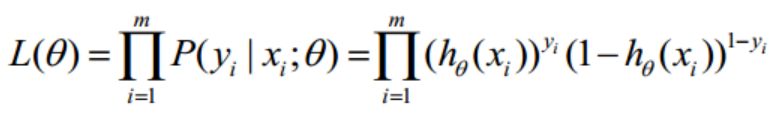
对数似然函数为:
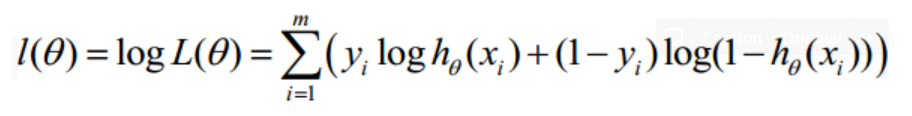
最大似然估计就是求使l(θ)取最大值时的θ,其实这里可以使用梯度上升法求解,求得的θ就是要求的最佳参数。
在Andrew Ng的课程中将J(θ)取为下式,即:
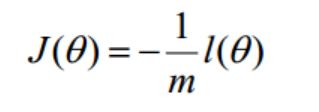
θ更新过程可以写成:
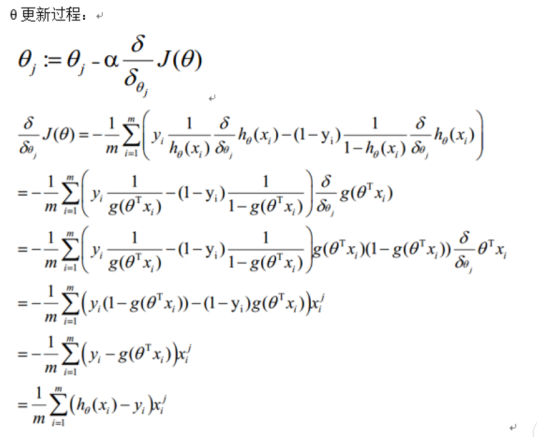
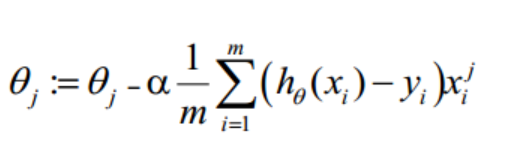
9.向量化
vectorization是使用矩阵计算来代替for循环,以简化计算过程,提高效率。
约定训练数据的矩阵形式如下,x的每一行为一条训练样本,而每一列为不同的特称取值:

g(A)的参数A为一列向量,所以实现g函数时要支持列向量作为参数,并返回列向量。
θ更新过程可以改为:
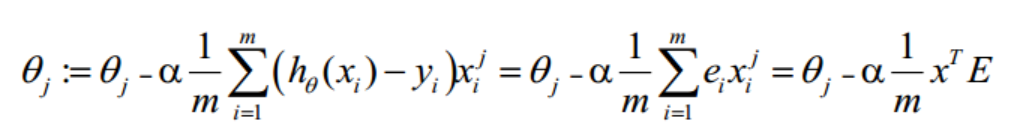
综上所述,Vectorization后θ更新的步骤如下:
求 A=x*θ
求 E=g(A)-y
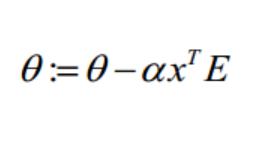
10.正则化
过拟合即是过分拟合了训练数据,使得模型的复杂度提高,泛化能力较差(对未知数据的预测能力)
下面左图即为欠拟合,中图为合适的拟合,右图为过拟合。
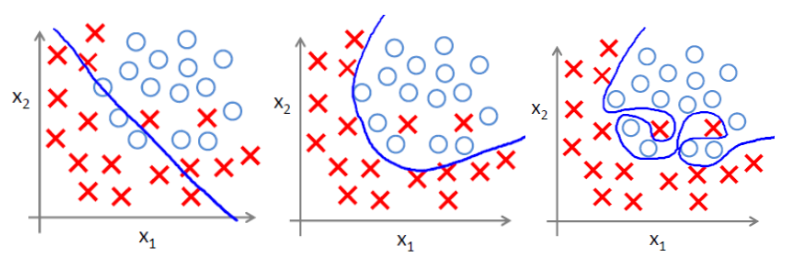
过拟合问题往往源自过多的特征
解决方法
- 可用人工选择要保留的特征
- 模型选择算法
- 保留所有特征,但减少θ的大小
正则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项或惩罚项。正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化项就越大。
正则项可以取不同的形式,在回归问题中取平方损失,就是参数的L2范数,也可以取L1范数。取平方损失时,模型的损失函数变为:
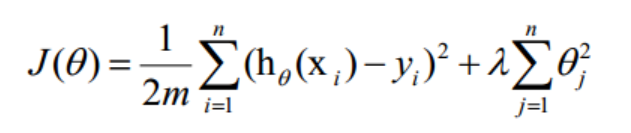
lambda是正则项系数:
- 如果它的值很大,说明对模型的复杂度惩罚大,对拟合数据的损失惩罚小,这样它就不会过分拟合数据,在训练数据上的偏差较大,在未知数据上的方差较小,但是可能出现欠拟合的现象;
- 如果它的值很小,说明比较注重对训练数据的拟合,在训练数据上的偏差会小,但是可能会导致过拟合。
正则化后的梯度下降算法θ的更新变为:
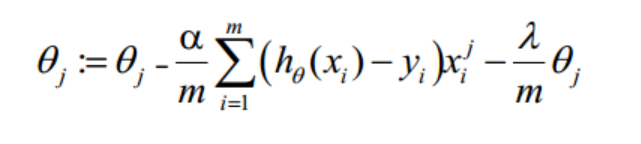
输入桩
支持单个csv文件输入。
输入端子1
- 端口名称:训练数据
- 输入类型:Csv文件
- 功能描述: 输入用于训练的数据
输出桩
支持sklearn模型输出。
输出端子1
- 端口名称:输出模型
- 输出类型:sklearn模型
- 功能描述: 输出训练好的模型用于预测
参数配置
交叉验证拆分数量
- 功能描述:交叉验证拆分数量
- 必选参数:是
- 默认值:(无)
penalty
- 功能描述:用于指定处罚时的规范
- 必选参数:是
- 默认值:I2
dual
- 功能描述:双重或者原始配方
- 必选参数:是
- 默认值:false
tol
- 功能描述:容忍度
- 必选参数:是
- 默认值:0.0001
C
- 功能描述:正则化强度的逆
- 必选参数:是
- 默认值:1
fit_intercept
- 功能描述:指定一个常量,是否加到决策函数中
- 必选参数:是
- 默认值:true
intercept_scaling
- 功能描述:截距缩放
- 必选参数:否
- 默认值:(无)
class_weight
- 功能描述:权重
- 必选参数:是
- 默认值:0.001
solver
- 功能描述:用于求解的算法
- 必选参数:是
- 默认值:lbfgs
multi_class
- 功能描述:多类
- 必选参数:是
- 默认值:auto
verbose
- 功能描述:将任意正数设置为详细
- 必选参数:是
- 默认值:0
warm_star
- 功能描述:是否调用上一次方案
- 必选参数:是
- 默认值:false
N jobs
- 功能描述:并行度
- 必选参数:否
- 默认值:(无)
l1_ratio
- 功能描述:弹性网络参数
- 必选参数:否
- 默认值:(无)
需要训练
- 功能描述:该模型是否需要训练,默认为需要训练。
- 必选参数:是
- 默认值:true
特征字段
- 功能描述:特征字段
- 必选参数:是
- 默认值:(无)
识别字段
- 功能描述:识别字段
- 必选参数:是
- 默认值:(无)
使用方法
- 将组件拖入到项目中
- 与前一个组件输出的端口连接(必须是csv类型)
- 点击运行该节点
