主成分分析解释方差(PCAExplainedVariance)使用文档
| 组件名称 | 主成分分析解释方差(PCAExplainedVariance) | ||
|---|---|---|---|
| 工具集 | 机器学习/算法设计/机器学习/评估/主成分分析解释方差(PCAExplainedVariance) | ||
| 组件作者 | 雪浪云-燕青 | ||
| 文档版本 | 1.0 | ||
| 功能 | 主成分分析解释方差(PCAExplainedVariance) | ||
| 镜像名称 | ml_components:3 | ||
| 开发语言 | Python |
组件原理
PCA(Principal Component Analysis) 是一种常见的数据分析方式,常用于高维数据的降维,可用于提取数据的主要特征分量。PCA通常用于降低大型数据集的维数,方法是数据集中的指标数量变少,并且保留原数据集中指标的大部分信息。总而言之:减少数据指标数量,保留尽可能多的信息
通过计算协方差矩阵的特征向量和特征值来确定数据的主成分。主成分定义:主成分是由初始变量的线性组合或混合构成的新变量。新变量是互不相关的,并且初始变量中的大部分信息被挤压或压缩到第一成分中。通俗来讲,十维数据给十个主成分,PCA试图将最大可能信息放在第一个组件中,然后第二组件中放置最大的剩余信息.
输入桩
支持sklearn文件输入。
输入端子1
- 端口名称:PCA模型
- 输入类型:sklearn文件
- 功能描述:输入PCA模型
输出桩
支持image文件输出。
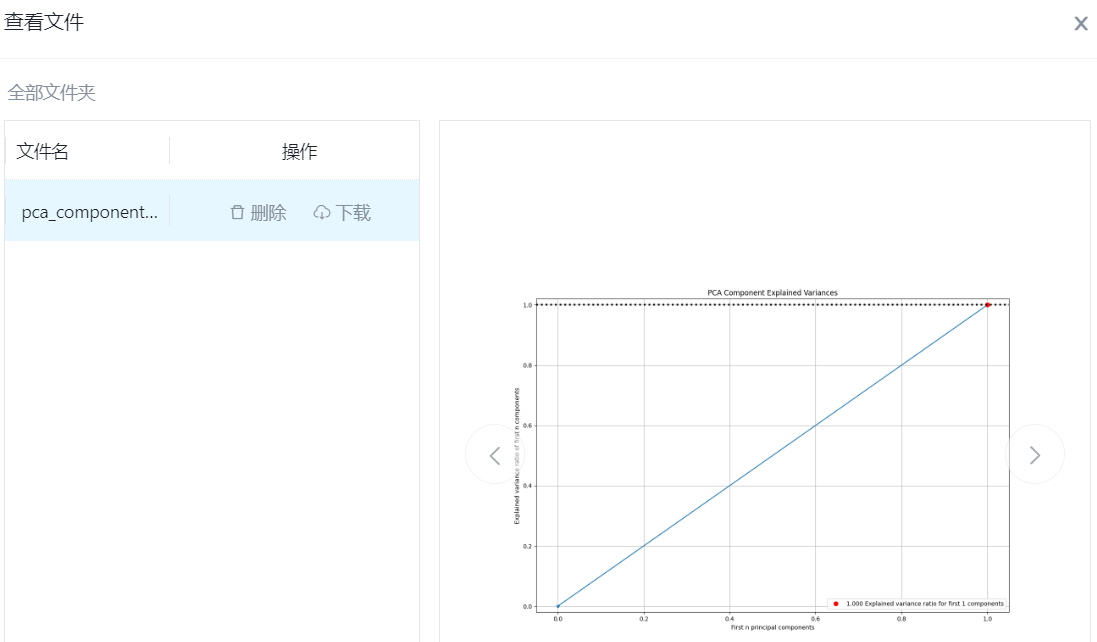
输出端子1
- 端口名称:输出图片
- 输出类型:image文件
- 功能描述:输出主成分分析解释方差图
参数配置
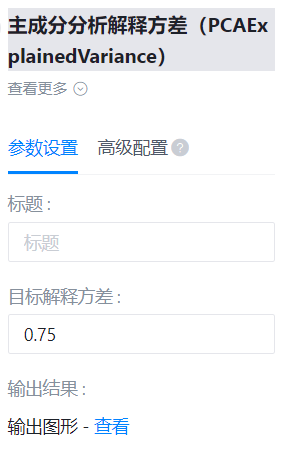
标题
- 功能描述:图像的标题
- 必选参数:是
- 默认值:(无)
目标解释方差
- 功能描述:目标解释方差
- 必选参数:是
- 默认值:0.75
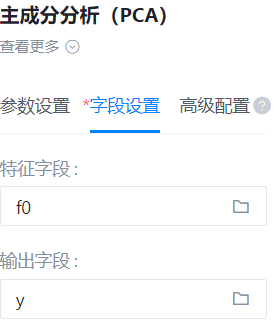
特征字段
- 功能描述:特征字段
- 必选参数:是
- 默认值:(无)
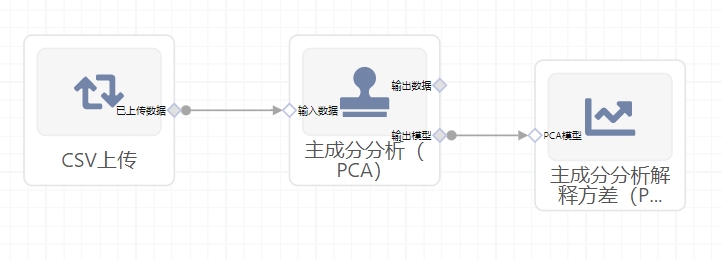
使用方法
- 将组件拖入到项目中
- 与前一个组件输出的端口连接(必须是csv类型)
- 点击运行该节点

测试用例
模板
右面板配置
查看结果