差分整合移动平均自回归
差分整合移动平均自回归属于算法组件中机器学习的一种时间序列回归组件。可以在“公共组件-算法设计-统计分析-时间序列分析”的分类中找到它。
原理
ARIMA模型（英语：Autoregressive Integrated Moving Average model），差分整合移动平均自回归模型，又称整合移动平均自回归模型（移动也可称作滑动），时间序列预测分析方法之一。ARIMA（p，d，q）中，AR是"自回归"，p为自回归项数；MA为"滑动平均"，q为滑动平均项数，d为使之成为平稳序列所做的差分次数（阶数）。“差分”一词虽未出现在ARIMA的英文名称中，却是关键步骤。
简介
ARIMA（p，d，q）模型是ARMA（p，q）模型的扩展。ARIMA（p，d，q）模型可以表示为：
其中L是滞后算子（Lag operator），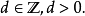
模型特点
不直接考虑其他相关随机变量的变化
ARIMA模型运用的流程
- 根据时间序列的散点图、自相关函数和偏自相关函数图识别其平稳性。
- 对非平稳的时间序列数据进行平稳化处理。直到处理后的自相关函数和偏自相关函数的数值非显著非零。
- 根据所识别出来的特征建立相应的时间序列模型。平稳化处理后，若偏自相关函数是截尾的，而自相关函数是拖尾的，则建立AR模型；若偏自相关函数是拖尾的，而自相关函数是截尾的，则建立MA模型；若偏自相关函数和自相关函数均是拖尾的，则序列适合ARMA模型。
- 参数估计，检验是否具有统计意义。
- 假设检验，判断（诊断）残差序列是否为白噪声序列。
- 利用已通过检验的模型进行预测。
使用
将差分整合移动平均自回归组件模块拖出，并找到想要使用的数据集与模型预测组件，分别与差分整合移动平均自回归组件组件连接。
预测结束后可以点击模型预测的查看结果，可以看到最后的prediction为最终的预测结果。
参数
点击差分整合移动平均自回归组件的参数设置选项，可以看到有参数可以手动设置。
trend:是否包含常数。“c”包括常数，“nc”没有常数。
method:这是最大似然方法。‘css-mle’,’mle’,’css’
maxiter:模型最大迭代次数。
disp:如果为真值则打印log。
order:模型的(p,q)阶为AR参数的个数，微分为MA参数的个数。
参考文献
https://baike.baidu.com/item/ARIMA模型 https://www.statsmodels.org/dev/generated/statsmodels.tsa.arima_model.ARIMA.html