跳到主要内容

自回归滑动平均（ARMA）

自回归滑动平均（ARMA）属于算法组件中机器学习的一种回归组件。可以在“公共组件-算法设计-统计分析-时间序列分析”的分类中找到它。

原理​

自回归滑动平均模型（英语：Autoregressive moving average model，简称：ARMA模型）。是研究时间序列的重要方法，由自回归模型（简称AR模型）与移动平均模型（简称MA模型）为基础“混合”构成。在市场研究中常用于长期追踪资料的研究，如：Panel研究中，用于消费行为模式变迁研究；在零售研究中，用于具有季节变动特征的销售量、市场规模的预测等。
ARMA模型(auto regressive moving average model)自回归滑动平均模型，模型参量法高分辨率谱分析方法之一。这种方法是研究平稳随机过程有理谱的典型方法，适用于很大一类实际问题。它比AR模型法与MA模型法有较精确的谱估计及较优良的谱分辨率性能，但其参数估算比较繁琐。
ARMA模型参数估计的方法很多：
如果模型的输入序列{u(n)}与输出序列{a(n)}均能被测量时，则可以用最小二乘法估计其模型参数，这种估计是线性估计，模型参数能以足够的精度估计出来；
许多谱估计中，仅能得到模型的输出序列{x(n）}，这时，参数估计是非线性的，难以求得ARMA模型参数的准确估值。从理论上推出了一些ARMA模型参数的最佳估计方法，但它们存在计算量大和不能保证收敛的缺点。因此工程上提出次最佳方法，即分别估计AR和MA参数，而不像最佳参数估计中那样同时估计AR和MA参数，从而使计算量大大减少。

使用​

将自回归滑动平均（ARMA）模块拖出，并找到想要使用的数据集与模型预测组件，分别与自回归滑动平均（ARMA）组件连接。 image.png 预测结束后可以点击模型预测的查看结果，可以看到最后的prediction为最终的预测结果。 image.png

参数​

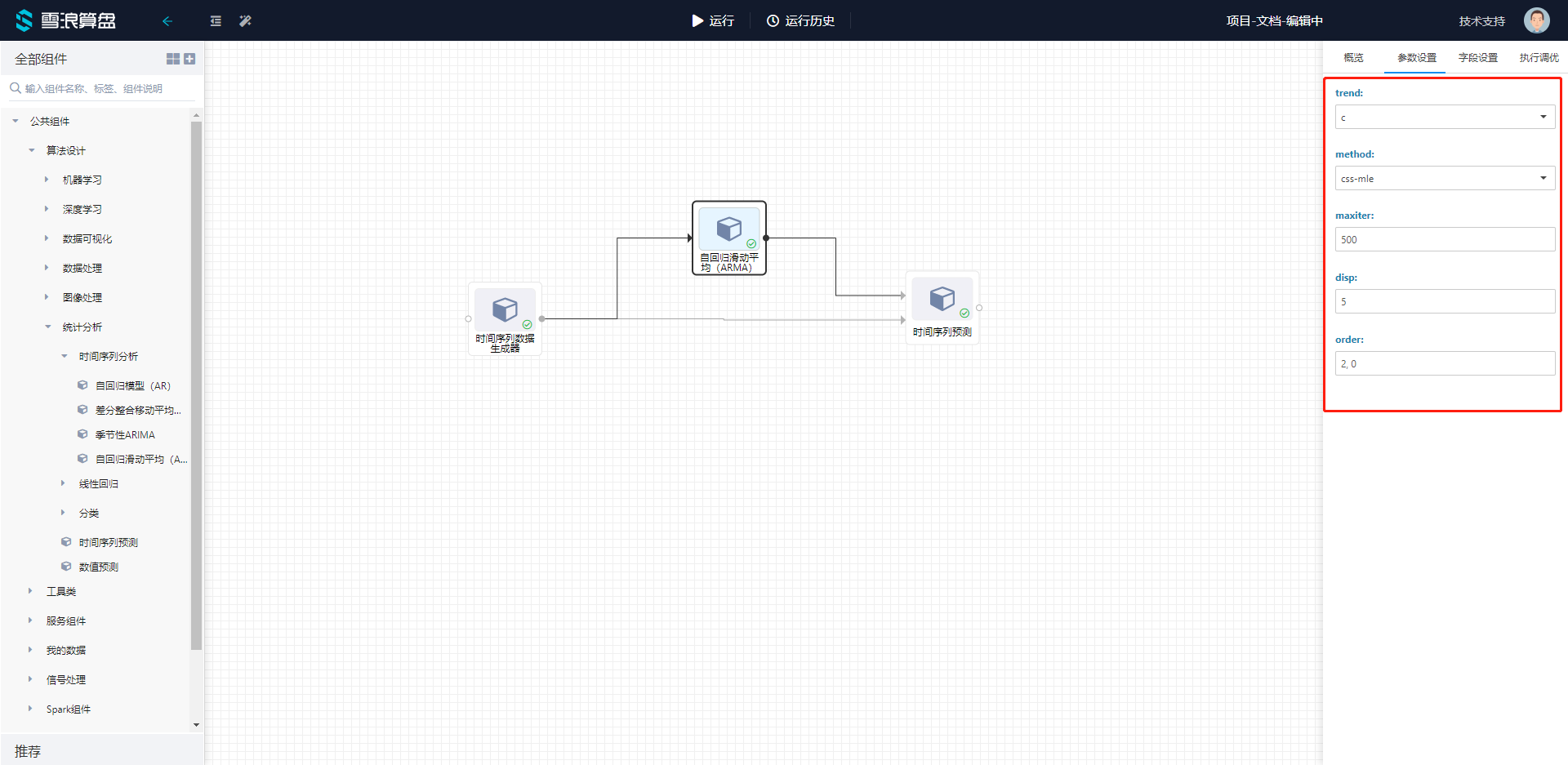
点击自回归滑动平均（ARMA）组件的参数设置选项，可以看到有参数可以手动设置。 image.png

trend:是否包含常数。“c”包括常数，“nc”没有常数。
method:这是最大似然方法。‘css-mle’,’mle’,’css’
maxiter:模型最大迭代次数。
disp:如果为真值则打印log。
order:模型的(p,q)阶为AR参数的个数，微分为MA参数的个数。

参考文献​

https://baike.baidu.com/item/ARMA%E6%A8%A1%E5%9E%8B/8048415?fr=aladdin https://www.statsmodels.org/dev/generated/statsmodels.tsa.arima_model.ARMA.html