季节性ARIMA

季节性ARIMA属于算法组件中机器学习的一种回归组件。可以在“公共组件-算法设计-统计分析-时间序列分析”的分类中找到它。

原理

概述

ARIMA模型的全称叫做自回归移动平均模型，全称是(Autoregressive Integrated Moving Average Model)。也记作ARIMA(p,d,q)，是统计模型(statistic model)中最常见的一种用来进行时间序列预测的模型。采用ARIMA模型预测时序数据，必须是稳定的（平稳性），如果不稳定的数据，是无法捕捉到规律的。比如股票数据用ARIMA无法预测的原因就是股票数据是非稳定的，常常受政策和新闻的影响而波动。

ARIMA模型原理

AR
描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测
自回归模型必须满足平稳性的要求
p阶自回归过程的公式定义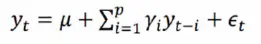： yt是当前值 u是常数项 P是阶数 ri是自相关系数 et是误差
自回归模型的限制
1、自回归模型是用自身的数据进行预测
2、必须具有平稳性
3、必须具有相关性，如果自相关系数（φi）小于0.5，则不宜采用
4、自回归只适用于预测与自身前期相关的现象
MA
移动平均模型关注的是自回归模型中的误差项的累加 
q阶自回归过程的公式定义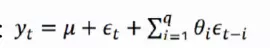： 移动平均法能有效地消除预测中的随机波动
ARMA
ARMA是自回归模型和移动平均模型的结合 ARIMA
I是差分模型，ARIMA是经过差分后的ARMA模型，保证了数据的稳定性。

使用

将季节性ARIMA模块拖出，并找到想要使用的数据集与模型预测组件，分别与季节性ARIMA组件连接。

预测结束后可以点击模型预测的查看结果，可以看到最后的prediction为最终的预测结果。

参数

点击季节性ARIMA组件的参数设置选项，可以看到有参数可以手动设置。

trend:控制确定性趋势多项式A(t)的参数。 ‘n’,’c’,’t’,’ct’。
method:该方法确定了来自scipy的哪个求解器。优化有：'newton'，' bfgs '， ' lbfgs '， 'powell'，' cg '， ' ncg '， ' basinhopping '。
maxiter:模型最大迭代次数。
disp:如果为真值则打印log。
order:模型的(p,q)阶为AR参数的个数，微分为MA参数的个数。
seasonal order:(P,D,Q,s)的顺序为AR参数，差分，MA参数和周期性。
measurement error:是否假设含有测量误差。
time varying regression:当提供解释变量exog以选择是否允许回归系数随时间变化。
mle regression:变量回归系数的估计是否通过卡尔曼滤波器。
trend offset:开始时间趋势值的偏移量。

参考文献

https://baike.baidu.com/item/ARIMA%E6%A8%A1%E5%9E%8B/10611682?fr=aladdin https://www.jianshu.com/p/91a931d8d92f https://www.statsmodels.org/dev/generated/statsmodels.tsa.statespace.sarimax.SARIMAX.html