3分类问题概率校准模板
下图为项目总览:
 项目可以分为四个部分:
项目可以分为四个部分:
- 第一部分,数据生成,分别生成训练数据,校准数据以及测试数据
import numpy as np
import pandas
from sklearn.datasets import make_blobs
import suanpan
from suanpan.app import app
from suanpan.app.arguments import Csv
def createDataFrame(X, y):
featureCount = X.shape[1]
featureColumns = ["feature_{}".format(i) for i in range(featureCount)]
labelColumns = ["label"]
features = pandas.DataFrame(X, columns=featureColumns)
label = pandas.DataFrame(y, columns=labelColumns)
return pandas.concat([features, label], axis=1, join_axes=[features.index])
@app.output(Csv(key="outputData1"))
@app.output(Csv(key="outputData2"))
@app.output(Csv(key="outputData3"))
@app.output(Csv(key="outputData4"))
def Demo(context):
args = context.args
np.random.seed(0)
# Generate data
X, y = make_blobs(n_samples=1000, n_features=2, random_state=42, cluster_std=5.0)
X_train, y_train = X[:600], y[:600]
X_valid, y_valid = X[600:800], y[600:800]
X_train_valid, y_train_valid = X[:800], y[:800]
X_test, y_test = X[800:], y[800:]
return (
createDataFrame(X_train, y_train),
createDataFrame(X_valid, y_valid),
createDataFrame(X_train_valid, y_train_valid),
createDataFrame(X_test, y_test),
)
if __name__ == "__main__":
suanpan.run(app)
- 第二部分,模型训练
- 随机森林分类模型
- 参数:n_estimators=25
- 随机森林分类模型加上概率校准分类模型
- 随机森林参数:n_estimators=25
- 概率校准模型参数:method=sigmoid,prefit=True
- 随机森林分类模型
- 第三部分,计算两种模型的log loss以及预测概率
import joblib
from sklearn.metrics import log_loss
import suanpan
from suanpan.app import app
from suanpan.app.arguments import Csv, File, Json, ListOfString, Npy, String
@app.input(Csv(key="inputData1", alias="inputData", required=True))
@app.input(
File(
key="inputModel2", alias="inputModel", name="model", type="model", required=True
)
)
@app.column(ListOfString(key="param1", alias="featureColumns", required=True))
@app.column(String(key="param2", alias="labelColumn", required=True))
@app.output(Json(key="outputData1"))
@app.output(Npy(key="outputData2"))
def Demo(context):
args = context.args
df = args.inputData
clf = joblib.load(args.inputModel)
clf_probs = clf.predict_proba(df[args.featureColumns].values)
score = log_loss(df[args.labelColumn].values, clf_probs)
return {"score": score}, clf_probs
if __name__ == "__main__":
suanpan.run(app)
- 第四部分,概率校准图解
- Sigmoid校准图解
import os
import joblib
import numpy as np
from matplotlib import pyplot as plt
import suanpan
from suanpan.app import app
from suanpan.app.arguments import File, Folder
TMP_FOLDER = "/tmp/result"
@app.input(
File(
key="inputModel1",
alias="calibratedModel",
name="model",
type="model",
required=True,
)
)
@app.output(Folder(key="outputData1"))
def Demo(context):
args = context.args
if not os.path.exists(TMP_FOLDER):
os.makedirs(TMP_FOLDER)
calibratedModel = joblib.load(args.calibratedModel)
# Illustrate calibrator
plt.figure(figsize=(12.8, 9.6))
colors = ["r", "g", "b"]
# generate grid over 2-simplex
p1d = np.linspace(0, 1, 20)
p0, p1 = np.meshgrid(p1d, p1d)
p2 = 1 - p0 - p1
p = np.c_[p0.ravel(), p1.ravel(), p2.ravel()]
p = p[p[:, 2] >= 0]
calibratedClassifier = calibratedModel.calibrated_classifiers_[0]
prediction = np.vstack(
[
calibrator.predict(this_p)
for calibrator, this_p in zip(calibratedClassifier.calibrators_, p.T)
]
).T
prediction /= prediction.sum(axis=1)[:, None]
# Plot modifications of calibrator
for i in range(prediction.shape[0]):
plt.arrow(
p[i, 0],
p[i, 1],
prediction[i, 0] - p[i, 0],
prediction[i, 1] - p[i, 1],
head_width=1e-2,
color=colors[np.argmax(p[i])],
)
# Plot boundaries of unit simplex
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], "k", label="Simplex")
plt.grid(False)
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], "k", alpha=0.2)
plt.plot([0, 0 + (1 - x) / 2], [x, x + (1 - x) / 2], "k", alpha=0.2)
plt.plot([x, x + (1 - x) / 2], [0, 0 + (1 - x) / 2], "k", alpha=0.2)
plt.title("Illustration of sigmoid calibrator")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
plt.savefig(os.path.join(TMP_FOLDER, "calibration.png"), format="png")
return TMP_FOLDER
if __name__ == "__main__":
suanpan.run(app)
效果图如下:
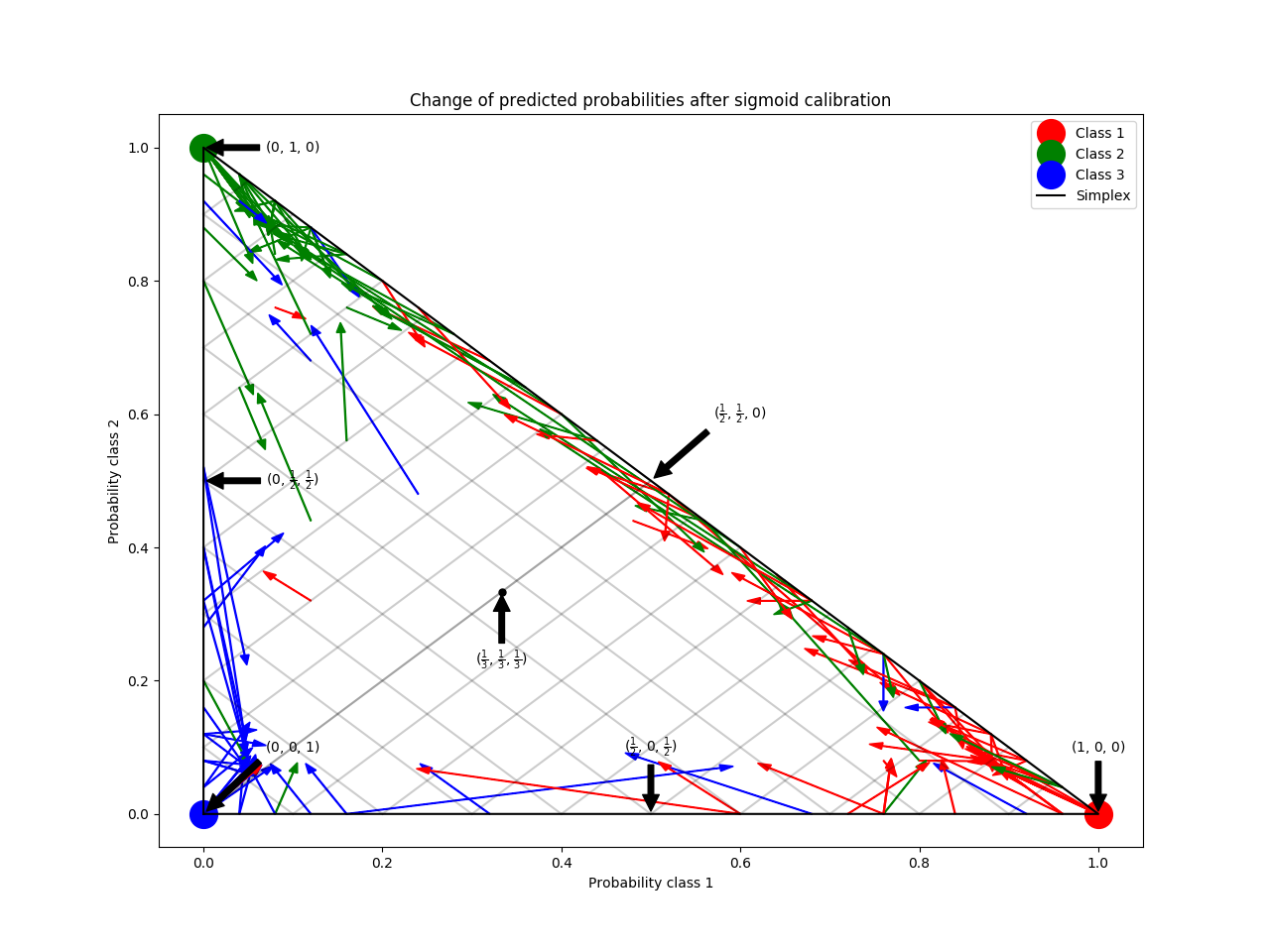
- Sigmoid校准后预测概率的变化图
import os
from matplotlib import pyplot as plt
import suanpan
from suanpan.app import app
from suanpan.app.arguments import Csv, Folder, Npy, String
TMP_FOLDER = "/tmp/result"
@app.input(Npy(key="inputData1", alias="calibratedProbs", required=True))
@app.input(Npy(key="inputData2", alias="probs", required=True))
@app.input(Csv(key="inputData3", alias="testData", required=True))
@app.param(String(key="param1", alias="labelColumn", required=True))
@app.output(Folder(key="outputData1"))
def Demo(context):
args = context.args
if not os.path.exists(TMP_FOLDER):
os.makedirs(TMP_FOLDER)
calibratedProbs = args.calibratedProbs
probs = args.probs
yTest = args.testData[args.labelColumn].values
# Plot changes in predicted probabilities via arrows
plt.figure(figsize=(12.8, 9.6))
colors = ["r", "g", "b"]
for i in range(probs.shape[0]):
plt.arrow(
probs[i, 0],
probs[i, 1],
calibratedProbs[i, 0] - probs[i, 0],
calibratedProbs[i, 1] - probs[i, 1],
color=colors[yTest[i]],
head_width=1e-2,
)
# Plot perfect predictions
plt.plot([1.0], [0.0], "ro", ms=20, label="Class 1")
plt.plot([0.0], [1.0], "go", ms=20, label="Class 2")
plt.plot([0.0], [0.0], "bo", ms=20, label="Class 3")
# Plot boundaries of unit simplex
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], "k", label="Simplex")
# Annotate points on the simplex
plt.annotate(
r"($\frac{1}{3}$, $\frac{1}{3}$, $\frac{1}{3}$)",
xy=(1.0 / 3, 1.0 / 3),
xytext=(1.0 / 3, 0.23),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.plot([1.0 / 3], [1.0 / 3], "ko", ms=5)
plt.annotate(
r"($\frac{1}{2}$, $0$, $\frac{1}{2}$)",
xy=(0.5, 0.0),
xytext=(0.5, 0.1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($0$, $\frac{1}{2}$, $\frac{1}{2}$)",
xy=(0.0, 0.5),
xytext=(0.1, 0.5),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($\frac{1}{2}$, $\frac{1}{2}$, $0$)",
xy=(0.5, 0.5),
xytext=(0.6, 0.6),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($0$, $0$, $1$)",
xy=(0, 0),
xytext=(0.1, 0.1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($1$, $0$, $0$)",
xy=(1, 0),
xytext=(1, 0.1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($0$, $1$, $0$)",
xy=(0, 1),
xytext=(0.1, 1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
# Add grid
plt.grid(False)
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], "k", alpha=0.2)
plt.plot([0, 0 + (1 - x) / 2], [x, x + (1 - x) / 2], "k", alpha=0.2)
plt.plot([x, x + (1 - x) / 2], [0, 0 + (1 - x) / 2], "k", alpha=0.2)
plt.title("Change of predicted probabilities after sigmoid calibration")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
plt.legend(loc="best")
plt.savefig(os.path.join(TMP_FOLDER, "calibration.png"), format="png")
return TMP_FOLDER
if __name__ == "__main__":
suanpan.run(app)
效果图如下: